Self-attention(上)
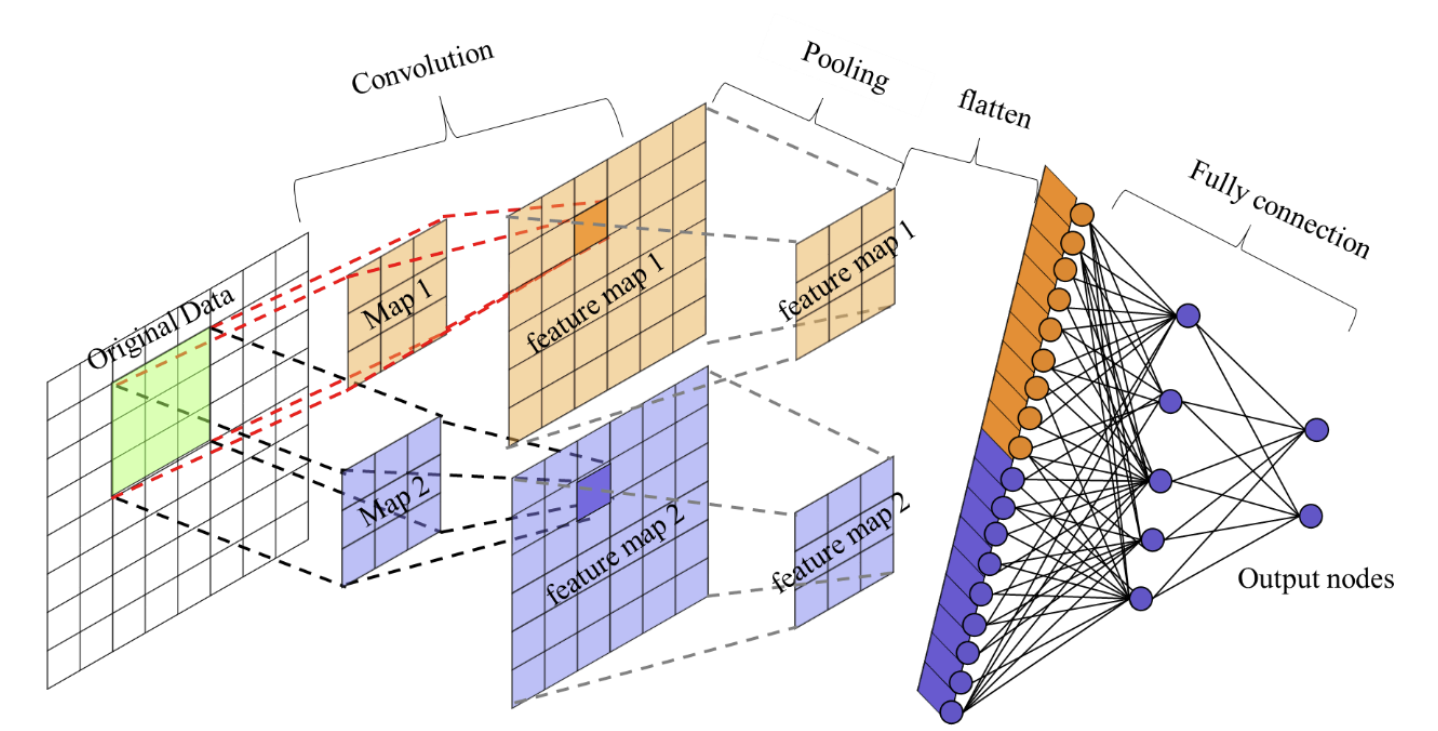
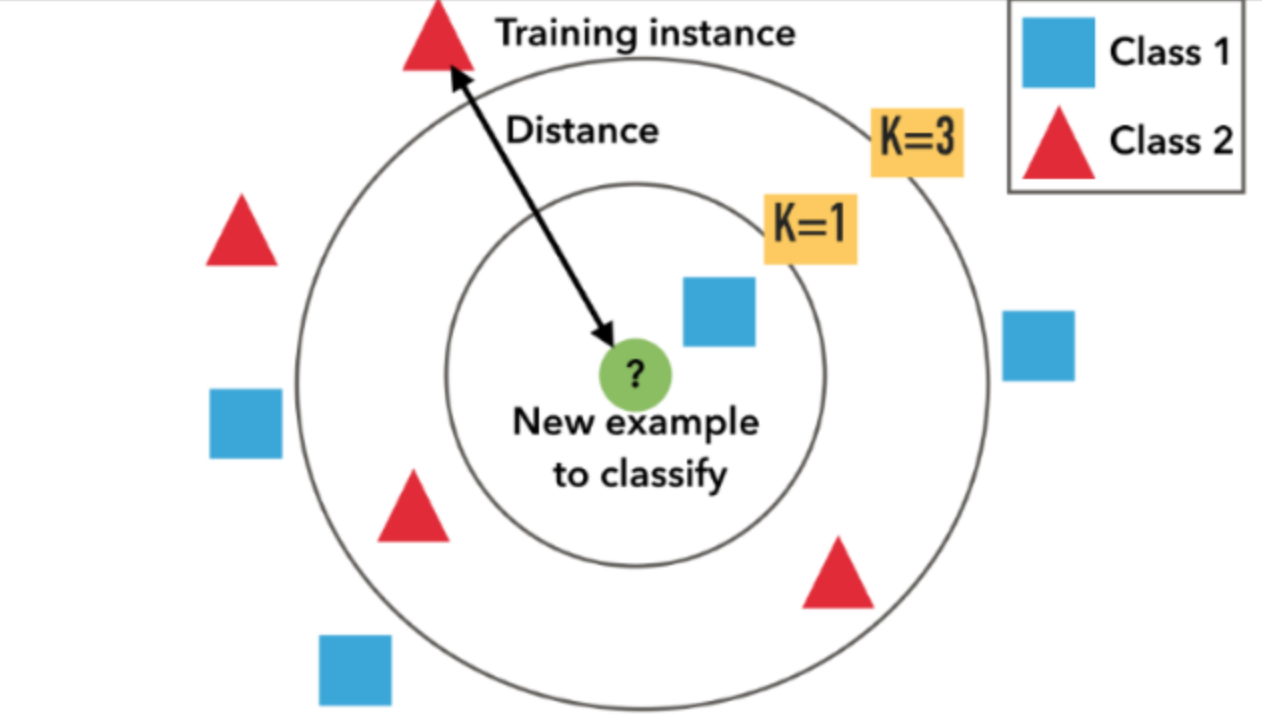
前言:当前已经学习的网络结构(感知机、支持向量机、KNN、CNN)的输入都是一个向量,而之前学习的如YouTube观看人数、城市新冠疫情预测等,其输入都可以看作一个向量,输出是一个数值时是回归问题(Regression),也可能是一个类别(Classification)
question:当输入是多个向量,而且向量的数量会改变时怎么办?——使用self-attention解决
Self-attention应用场景
文字处理
声音信号处理
图
分子
文字处理
- 输入:一个句子
- 每个句子的长度不一样,句子中词汇数目不一样
句子中的每一个词汇都描述成一个向量,那么model的输入就是一个向量集,而这个向量集的大小每次都不一样。
question:如何将一个词汇表示成向量?
方法1: One-Hot的Encoding

开一个很长的向量,定义每一个单词,很明显这样是不可行的。
同时这样的表示方法有一个非常严重的问题,它假设所有的词汇彼此之间都是没有关系的,从这个向量里面你看不到:Cat跟Dog都是动物所以他们比较接近,Cat跟Apple一个动物一个植物,所以他们比较不相像。这个向量里面,没有任何语义的信息。
方法2: Word Embedding
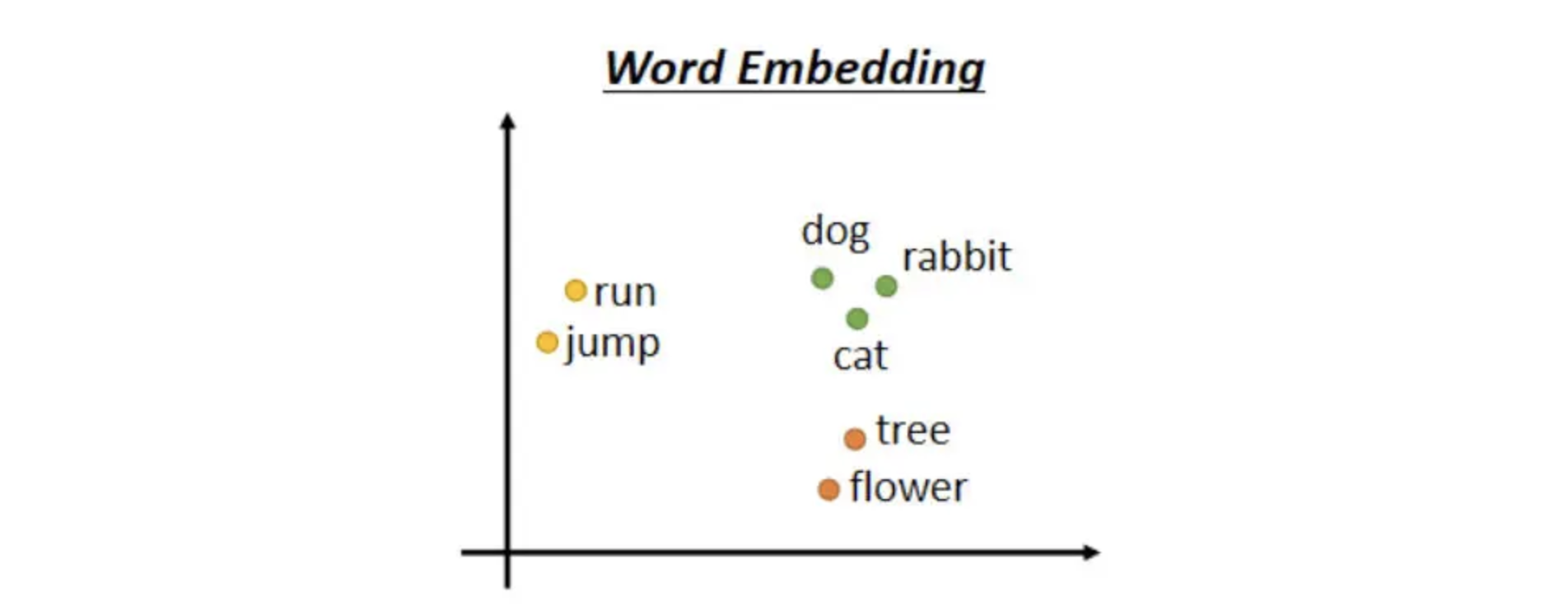
Word Embedding就是给每一个词汇一个向量,而这个向量是有语义的信息的,看图可以发现所有的动物可能聚集成一团,所有的植物可能聚集成一团,所有的动词可能聚集成一团。至于是怎么让他们分别汇聚的
可以看:Youtube:Unsupervised Learning - Word Embedding
B站:Unsupervised Learning - Word Embedding
声音信号处理
- 一段声音信号是一排向量,将一段声音信号取一个范围,这个范围就是一个window
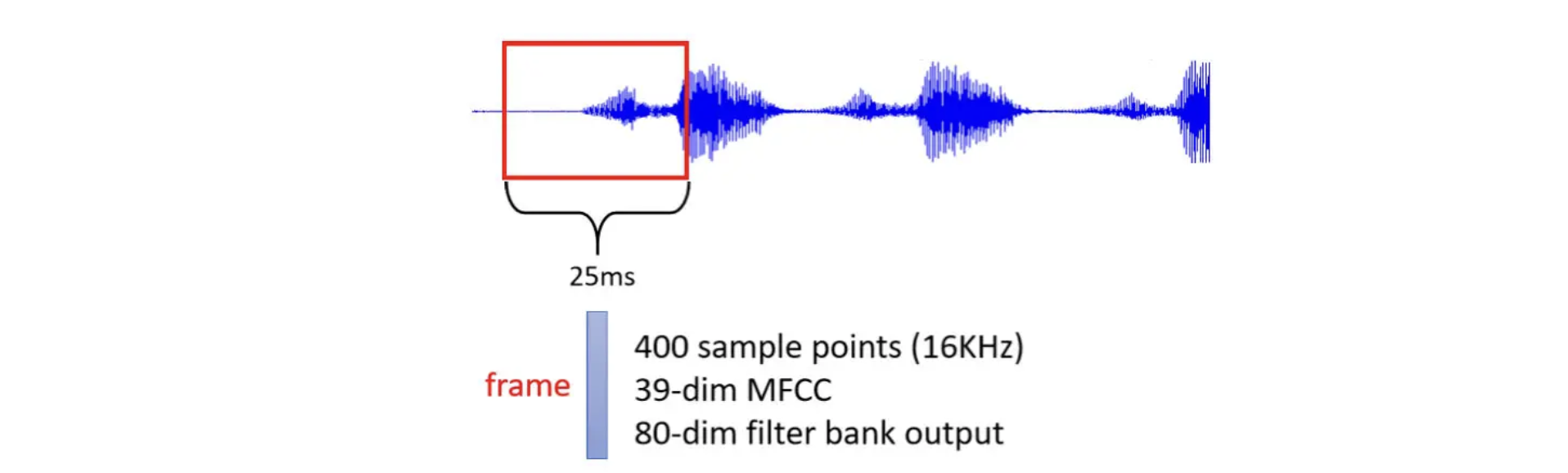
把窗口内的信息描述成一个向量,这个向量就叫做Frame,通常这个窗口的长度是25毫秒。
而把声音信号变成向量的方法很多,如MFCC
为了要描述一整段的声音信号,把这个Window往右移一点,通常移动的大小是10毫秒(前人测试所得)
- 所以1s的声音有100个向量,所以1min的声音就有100*60=6000个向量。所以语音其实很复杂的,一小段的声音,它里面包含的信息量其实是非常可观的。
图
一个图,也是一堆向量。例如Social Network这个图:
- 每个人可以看作一个节点,其中的工作、性别、年龄可以看作向量
分子信息
识别出分子是否具有毒性、是否亲水……

- 一个分子可以看作是一个Graph,分子上面的每一个球,也就是每一个原子,都可以表述成一个向量
一个原子可以用One-Hot Vector,来表示,氢就是1000,碳就是0100,氧是0010,所以一个分子就是一个Graph,它就是一堆向量。
输出类型
- 每一个向量都有一个对应的Label
- 词性判断
- 音标标注
- 一整个序列输入,只需要输出一个Label
- 情感分析,输出positive/negative,optimistic/pessimistic
- 算法决定输入多少个Label
- 人不知道应该输出多少个Label,机器要自己决定,应该要输出多少个Label,可能你输入是$N$个向量,输出可能是$N’$个Label,为什么是$N’$,机器自己决定。
- 这种任务又叫做sequence to sequence的任务
序列标注 Sequence Labeling
本篇记录的是输出类型中的第一种情况:输入跟输出数目一样多。这种情况又叫做序列标注(Sequence Labeling)。
在词性识别中:
$$
I\quad saw\quad a\quad saw(我看到一把锯子)
$$
如何识别出两个saw的词性?
可以把前后几个向量都串起来,一起丢到Fully-Connected的Network中进行识别得出结果,也就是我们说的,考虑上下文
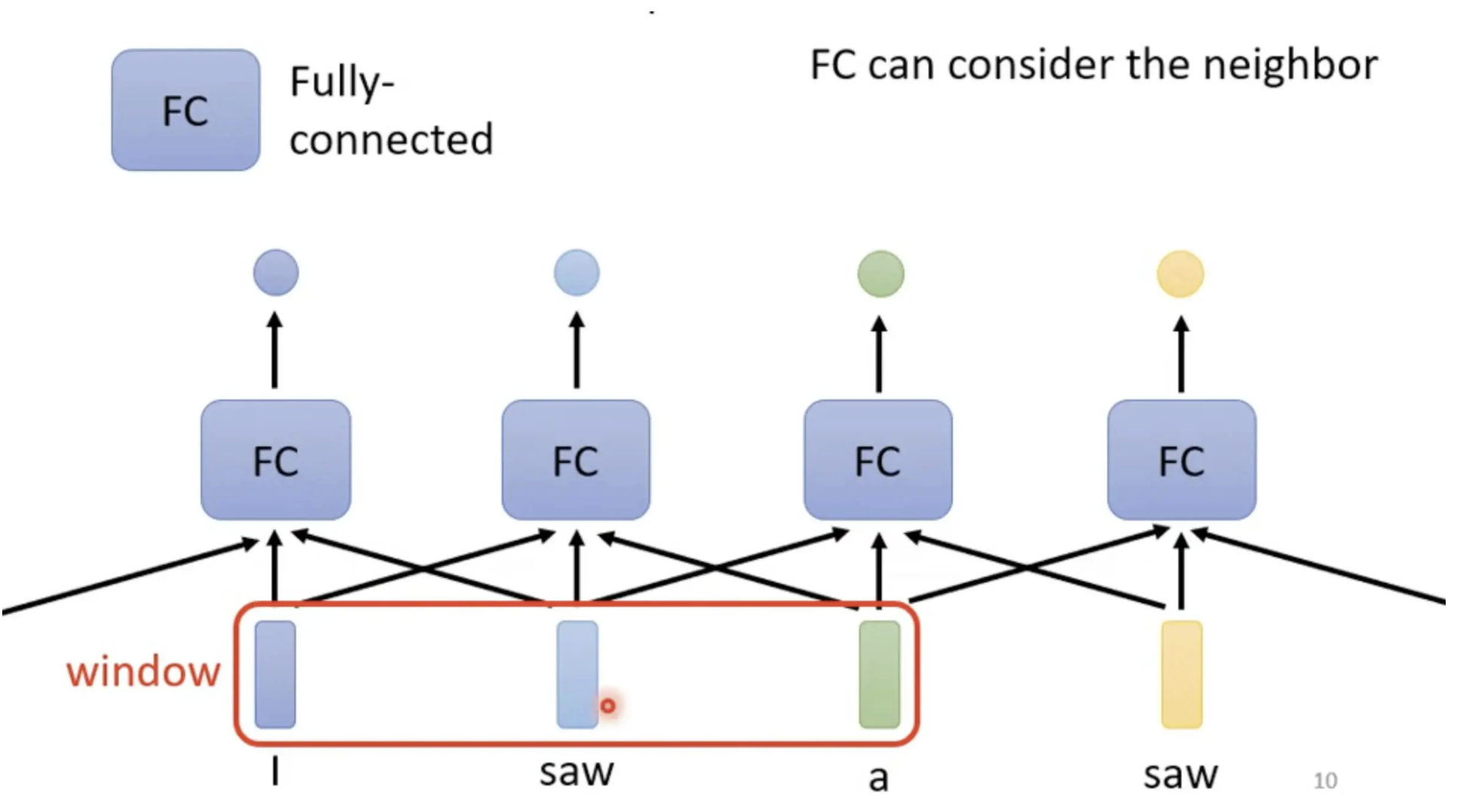
但是这样的方法是有局限性的,如果需要考虑整个序列时:
Sequence的长度是有长有短,输入给我们的Model的Sequence的长度,每次可能都不一样
或者说建立一个很大的窗口可以包容所有长度的序列,这意味着Fully-Connected的Network需要非常多的参数,那可能不只运算量很大,可能还容易Overfitting
既然如此,要解决上述问题,就可以考虑本篇要说的Self-attention技术了。
详解Self-attention
来源和总体思路
- 出自《Attention is all you need》,作者首次提到Transformer
self-attention的运作方式是一次性接受整个sequence的信息,self-attention输入几个向量,它就输出几个向量。
对于输出,也就是红色框内的向量,他们都是考虑一整个Sequence以后才得到,并不是一个普通的向量。
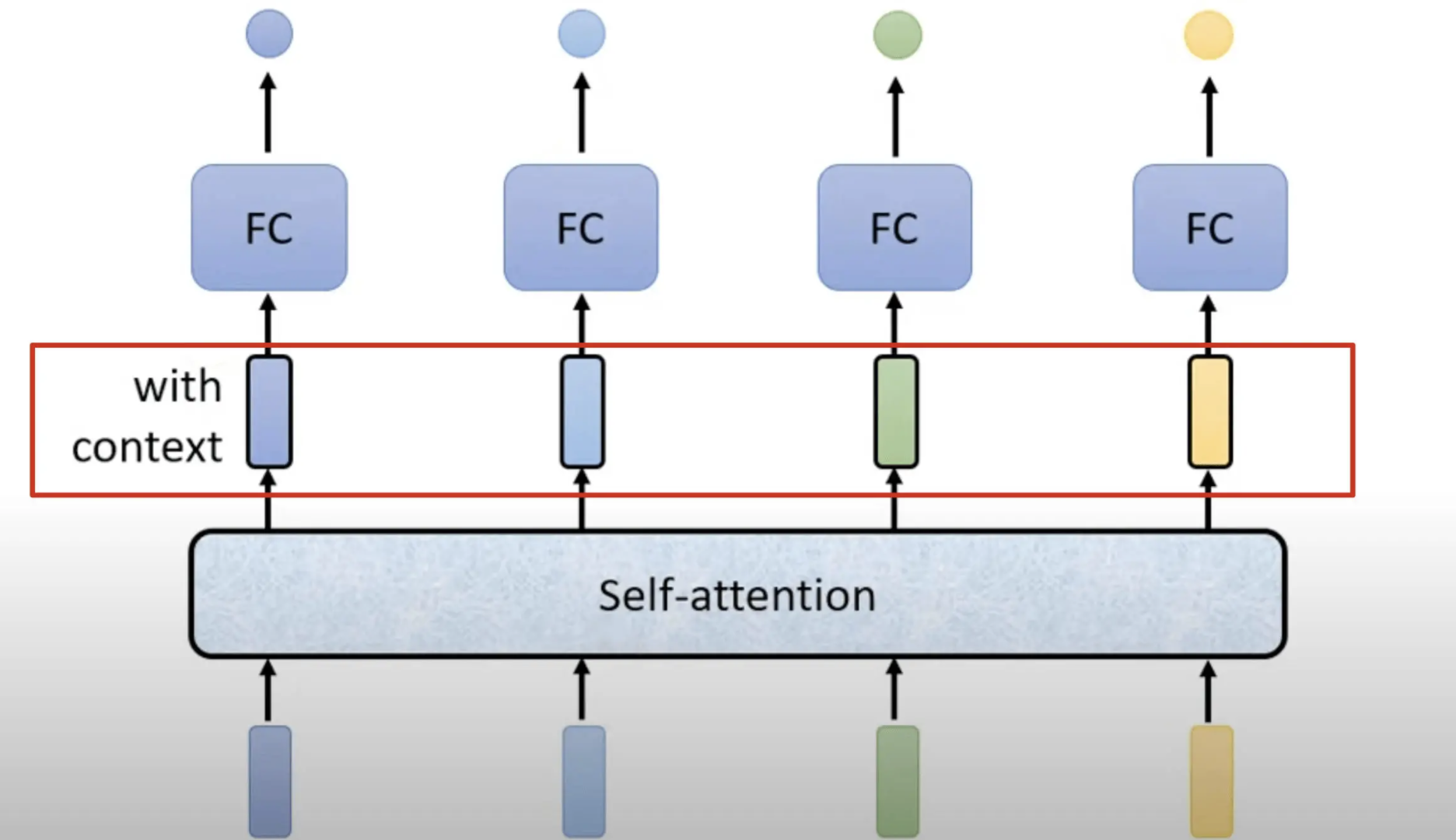
如此一来这个Fully-Connected的Network,就不再只是一个只考虑非常小的范围,或很小一个Window的网络,而是考虑整个Sequence的信息并决定输出什么样的结果,这就是Self-Attention,而且Self-Attention不是只能用一次,可以叠加很多次。
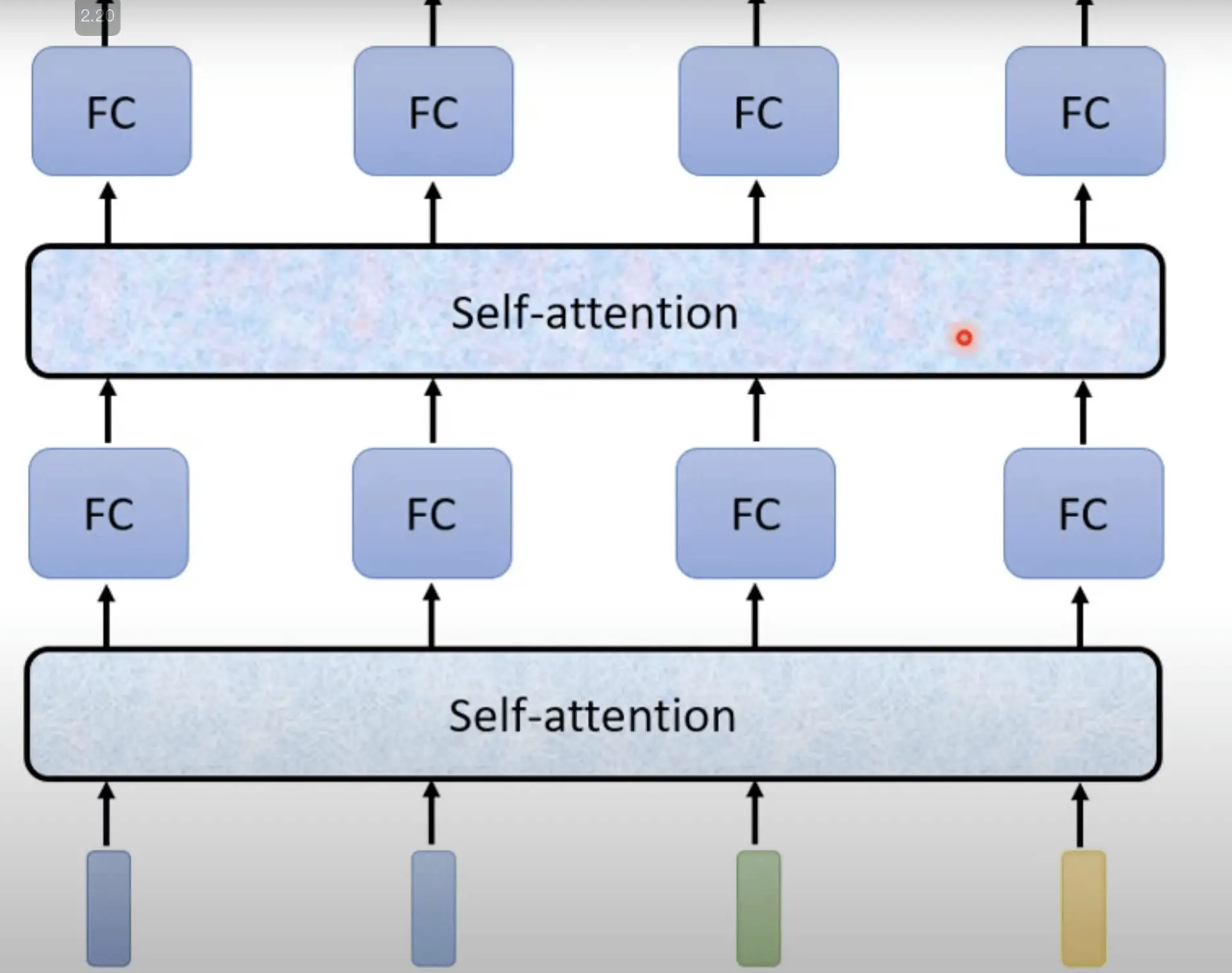
可以把Fully-Connected的Network,跟Self-Attention交替使用
- Self-Attention处理整个Sequence的信息
- Fully-Connected的Network,专注于处理某一个位置的信息
- 再用Self-Attention把整个Sequence信息再处理一次
- 然后交替使用Self-Attention跟Fully-Connected
实现过程
Self-Attention的输入,它就是一串的向,这个向量可能整个Network的输入,也可能是某个Hidden Layer的输出。此处用$a^i$表示
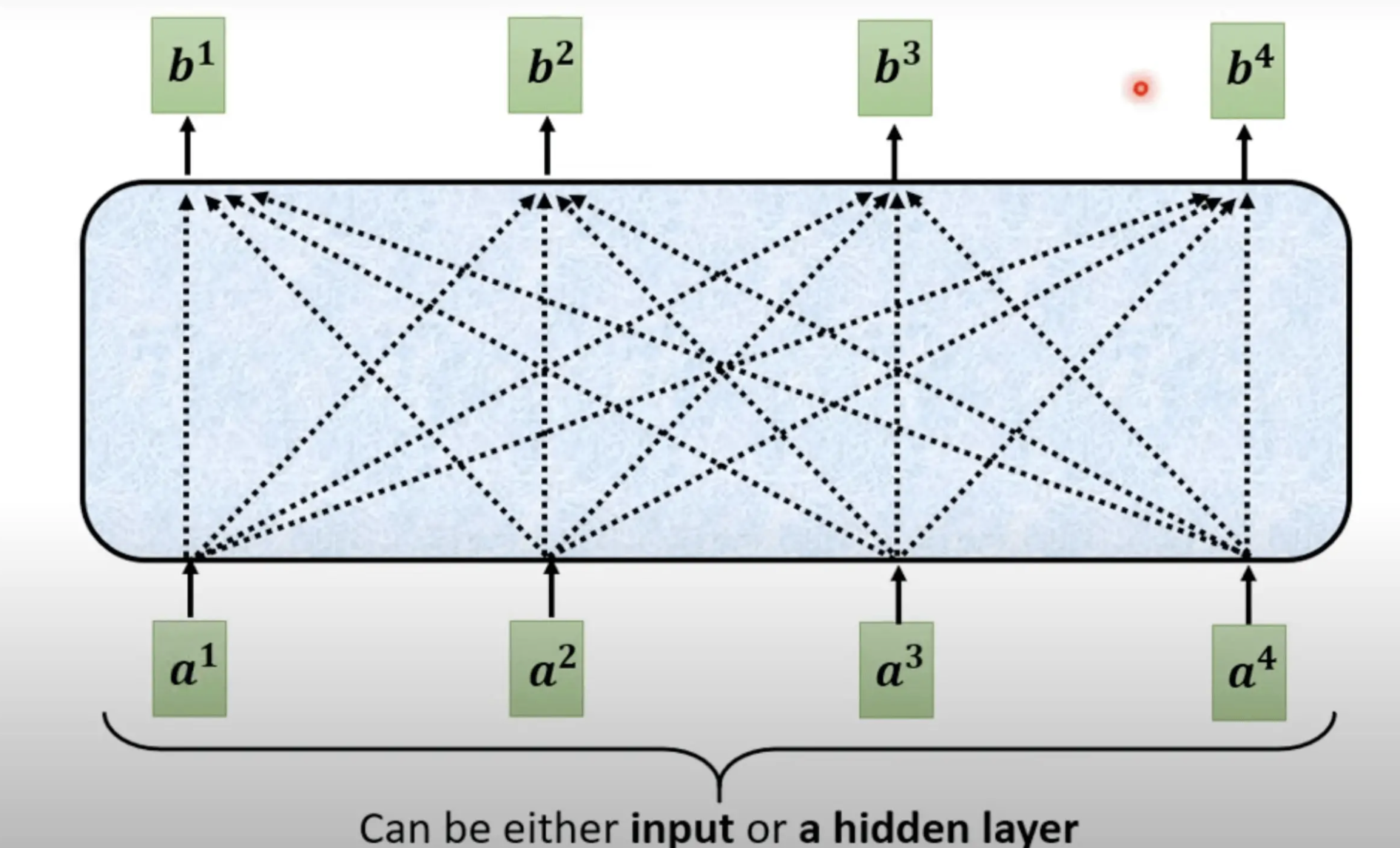
question: 从self-attention输入的每一个$b^i$都是考虑了所有$a^i$而得出的,那么生成$b^i$的规则是什么呢?
计算attention的模组
对于$a^1$,要从整个序列中找出与其相关性较大的其他向量$a^n$(find the relevant vectors in a sequence)
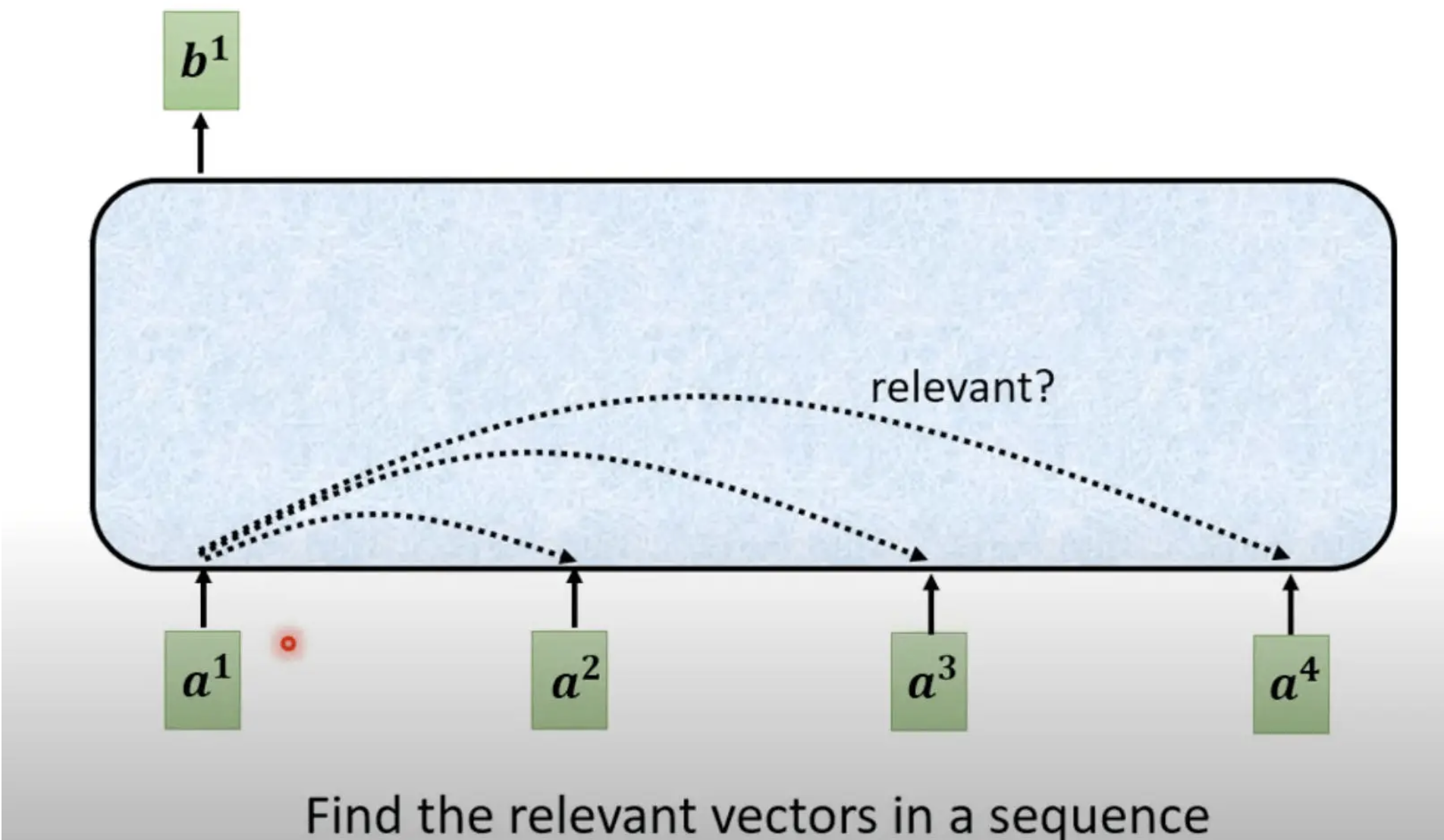
计算每一个向量$a^n$与$a^1$的关联程度,用一个数值$a$来表示,计算关联程度的过程,就是计算attention模组的过程
计算过程
计算attention的模组,就是输入两个向量,然后输出$a$的数值。
计算方法有各种各样的做法(论文学习:dot product、additive等),总之目的就是计算各个向量的关联程度。
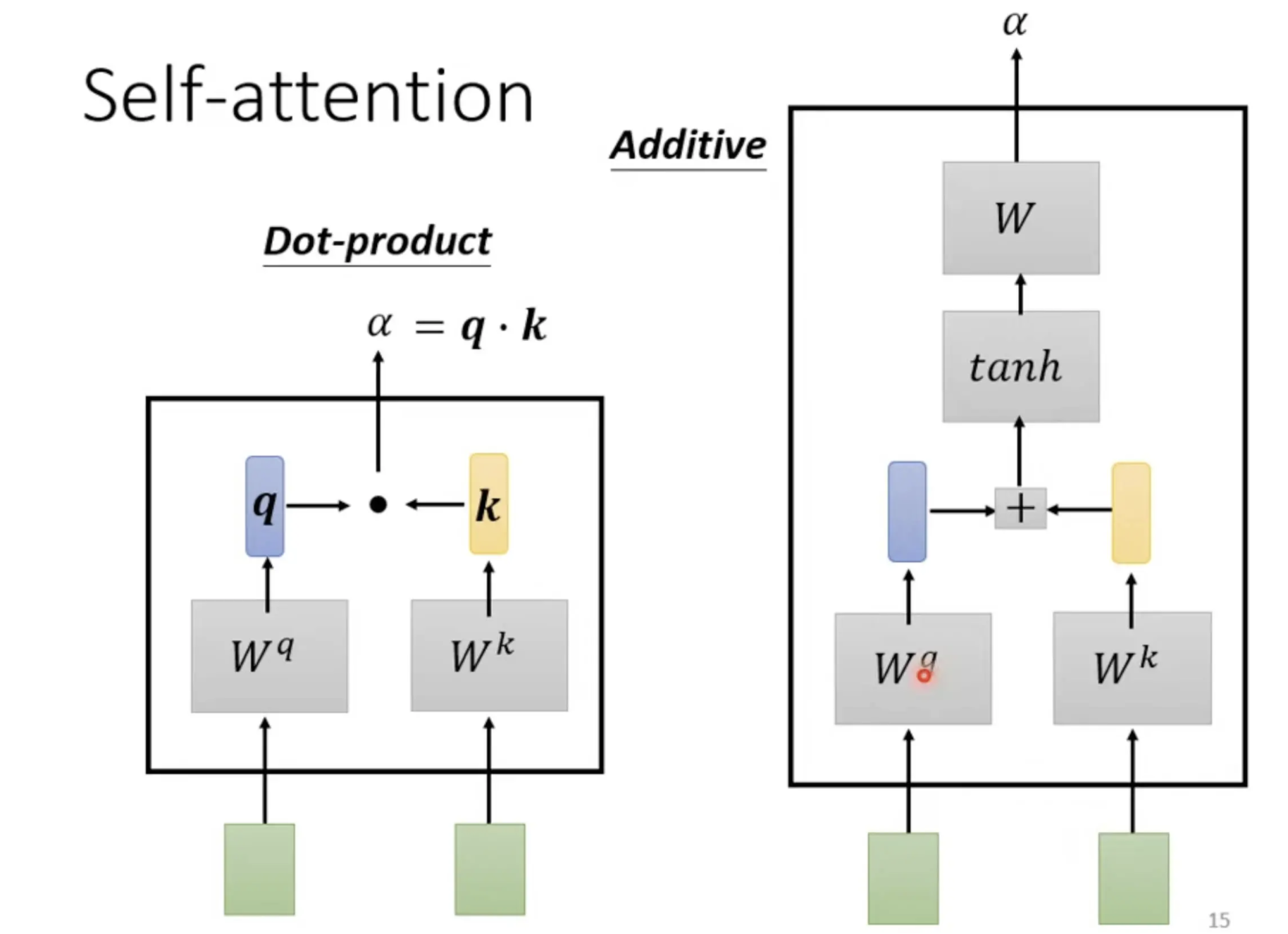
dot product
首先,输入的这两个向量分别乘上两个不同的矩阵,左边这个向量乘上$W^q$矩阵得到矩阵$q$,右边的向量乘上$W^k$矩阵得到矩阵$k$,然后把矩阵$q$跟矩阵$k$做dot product,也就是把他们做element-wise 的相乘,再全部加起来以后就得到一个 scalar,这个scalar就是矩阵$a$,这是一种计算$a$的方式。
ps:elementwise multiplication 直白翻译过来就是元素的智能乘积。例如
表示对每一个输入向量 $v$ 乘以一个给定的”权重”—— $w$向量。换句话说,就是通过一个乘子对数据集的每一列进行缩放。这个转换可以表示为如下的形式:
再直白一点,就是同位元素对应相乘。
Additive
首先,把同样这两个向量通过$W^q$, $W^k$得到$q$跟$k$,然后不做Dot-Product,而是把他们串起来,接着丢到Activation Function中,最后通过一个Transform,得到α。
以下采用dot product方法进行,也是用在Transformer里面的方法
把$a^1$分别与$a^2$、$a^3$、$a^4$计算他们之间的关联性,也就是计算他们之间的$a$,一般实际操作时,$q^1$会自己做query和key计算自己跟自己的关联性。
$q$ 代表Query,它就像是使用搜寻引擎,去搜寻相关文章时的关键字,所以叫做Query。
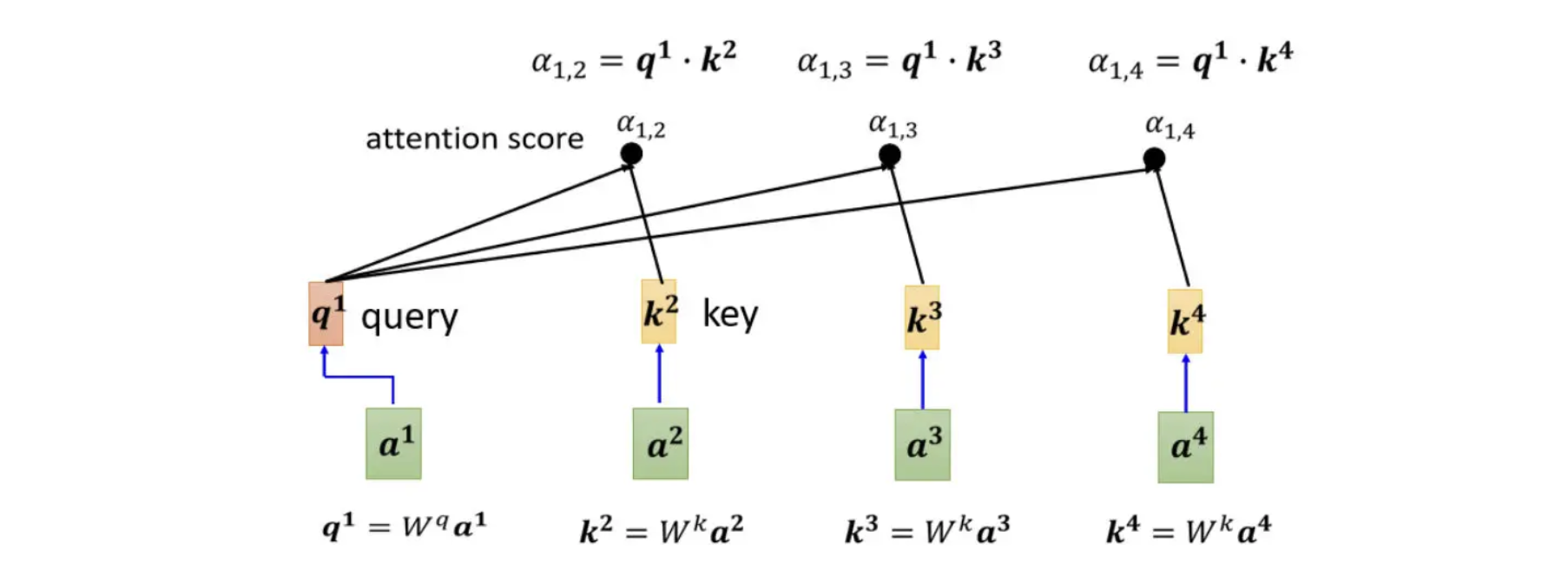
计算出$a^1$跟每一个向量的关联性以后,接下来会接入一个Soft-Max,但并不是非soft-max不可,也可以使用别的,例如说ReLU,总而言之使用什么Activation Function都行,以实际效果为评判标准
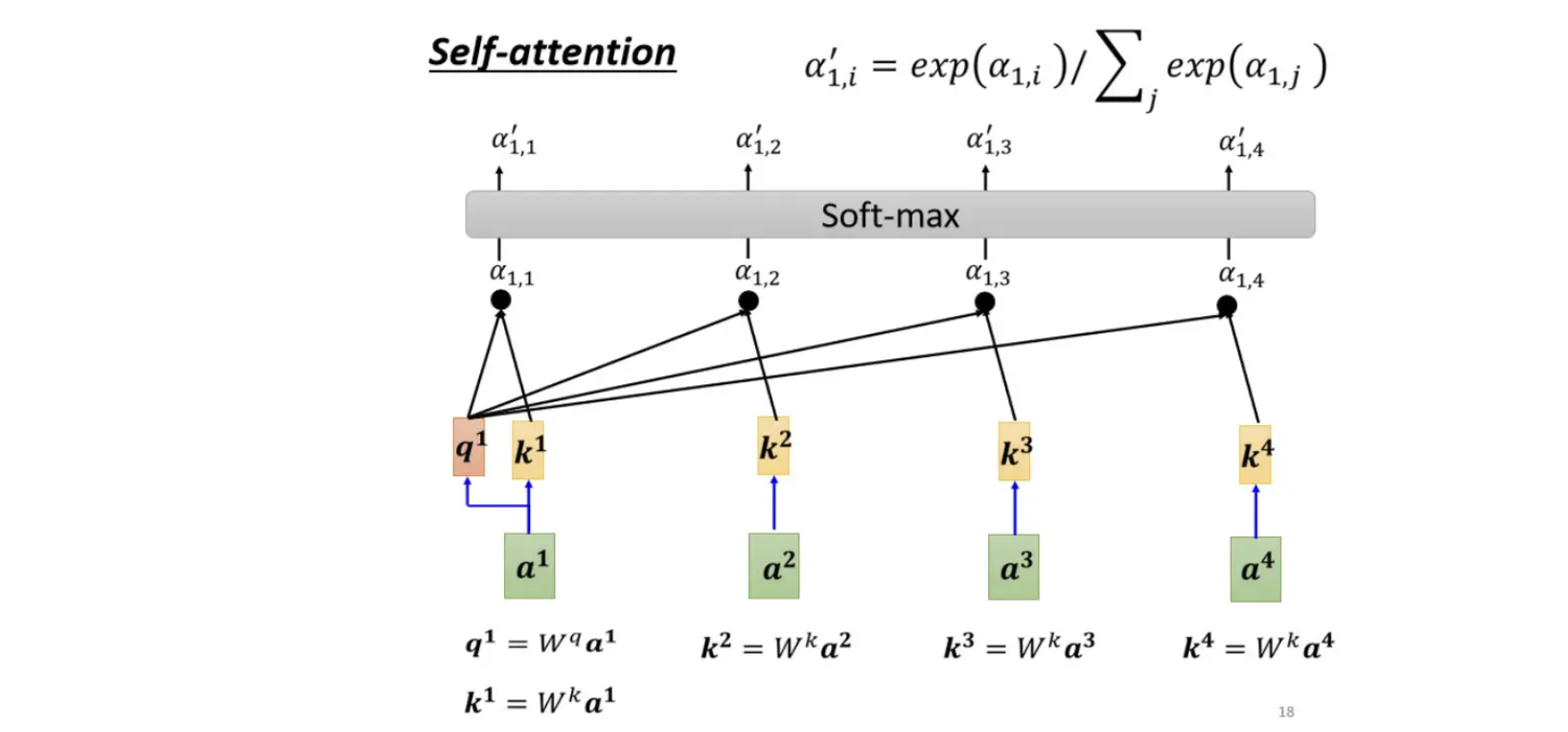
Soft-Max的输出就是一排α′,所以本来有一排α,通过Soft-Max就得到α′。
α′的作用及操作
求得α的初心是为了知道哪些向量跟$a^1$的关系较大,所以辗转得到的α′,是用于抽取出Sequence里面相关性高的向量。
那么具体要如何抽取呢?

首先把$a^1$到$a^4$(也就是每一个向量)乘上$W^v$得到新的向量,此处用$v^1,v^2,……$,表示
接下来把$v^1$到$v^4$每一个向量都乘上经过了激活函数Activation Function之后的attention score分数,也就是α′
再做累加,得到一个$b^1$
$$
b^1 = \sum_{i}a_{1,i}^`,v^i
$$
如果某一个向量得到的分数越高,比如说$a^1$和$a^2$的关联性很强,那么由$a^1$和$a^2$得到的α′的值自然就会很大,那么得到由各个α′与$v^i$相乘之后相加所得的$b^1$的值,就可能会比较接近于$v^2$,也就是说$v^2$占据了主导地位。
以上就是从一整个输入序列中求得$b^1$的方法。
但看完本篇难免会有一个问题:
文中提到的$W^q 、 W^k 、 W^v$都是什么?又从哪里来?
具体可看self-attention下篇。